[论文解读] Skip Lists: A Probabilistic Alternative to Balanced Trees

写在前面

跳跃表是一种可以替代平衡树的数据结构。跳跃表采用概率上的平衡而不是强制要求节点的平衡，使得其在插入和删除时更容易实现，而且具有更好的效率。由于跳跃表具有良好的性能和算法实现的简单性，被广泛应用于工程实践中，如redis、leveldb等。

本文是对William Pugh的论文Skip Lists: A Probabilistic Alternative to Balanced Trees的解读，主要介绍算法核心思想和算法实现，对于算法的时间和空间复杂度分析并不是本文的重点，这部分内容在论文中有详细介绍。

核心思想

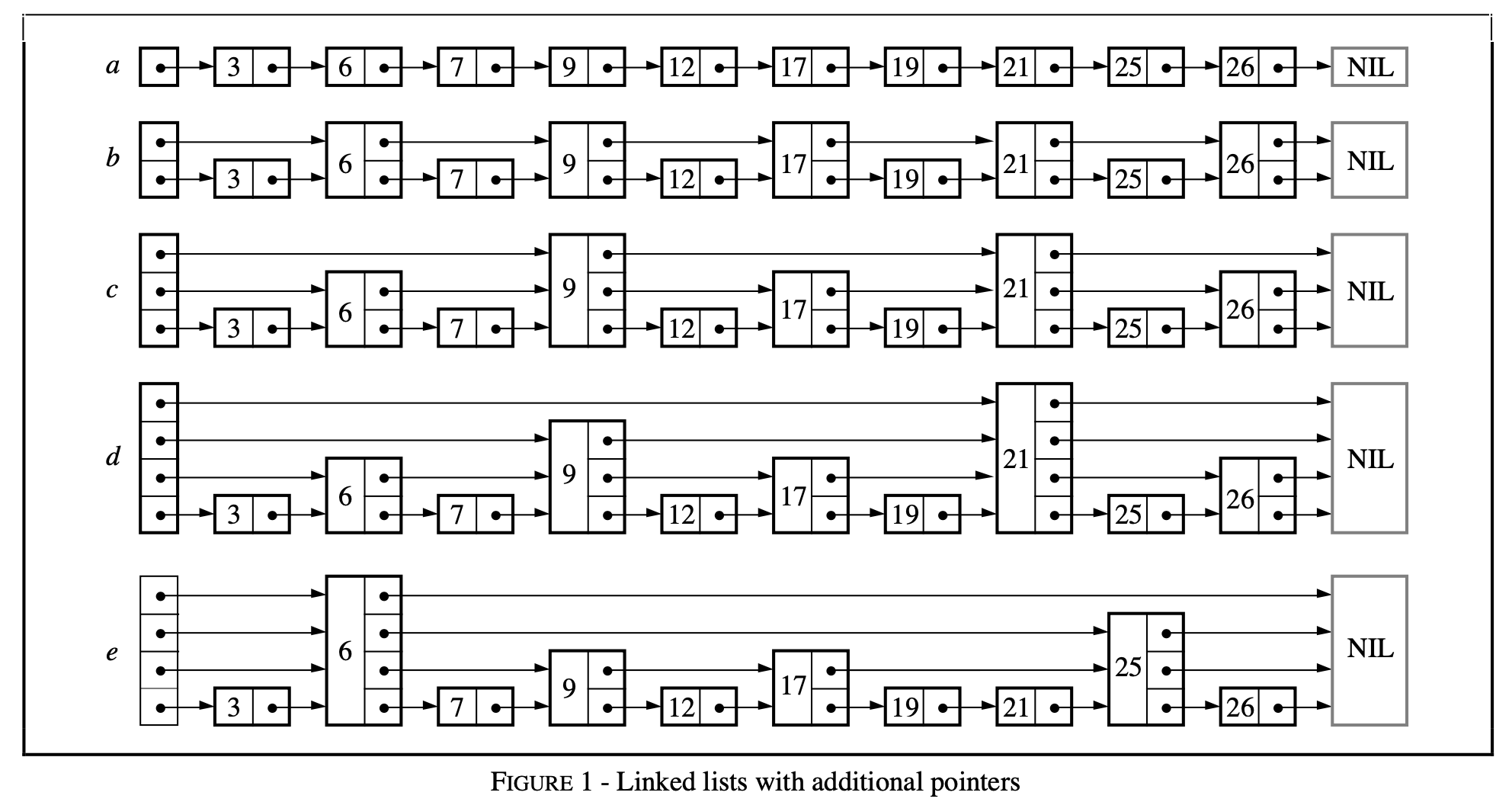
对于一个单链表而言，我们需要检查所有节点才能找到目标值（Figure 1a）。如果链表中的数有有序的，并且有一半的节点有一个额外的指针指向跨越一个节点（Figure 1b）。这样只需要检查⌈n/2⌉ + 1（n是链表的长度）个节点就可以找到目标值。同样，如果链表中的每第4个节点可以跨越4个节点（Figure 1c），那么只需要检查⌈n/4⌉ + 2 个节点就可以找到目标值。

推广到一般化，如果每第2ⁱ个节点有2ⁱ个向前指针，那么只需要检查⌈log₂ n⌉次就可以找到目标值（Figure 1d）。

是不是感兴跟二叉树很像，这种方式查找很快，但添加和删除即很慢。想象一下在链表中间插入一个节点，节点后面的所有指针都需要做调整。

一个节点如果包含k个向前指针，那么称这个节点为k层节点。通过上面的一般化分析，每第2ⁱ个节点有2ⁱ个向前指针，那么节点间的层级分布为：

50%的节点为1层
25%的节点为2层
12.5%的节点为3层
以此类推

跳跃表采用了一种概率算法。并不要求每第2ⁱ个节点有2ⁱ个向前指针，只是在概率上要求整体节点的层级符合上述分布。另外，节点的第i个向前指针并不需要指向第2^i-1个节点，而是指向下一个具有i层级的结点（Figure 1e）。这样做有什么好处呢？

这样可以让插入和删除只需要进行本地修改（O(1)时间复杂度）就可以完成。下面来看下具体的算法实现。

算法描述与实现

论文中定义L(n)表示含有n个节点的跳跃表的层级，表示为：

L(n) = log_1/pn

我们可以固定最大的层级和随机因子p，按照论文作者的建议，p设置为1/4是一个比较好的选择，这样如果最大层级MAX_LEVEL设置为32，则可以存储2⁶⁴个节点。

数据结构

随机因子P设置为0.25，最大层级MAX_LEVEL设置为32。为了简单起见，一个跳跃表节点使用一个int型表示要存储的数据，Forward[i]表示第i层的向前指针。跳跃表存储了头节点，并使用level维护跳跃表的层级。

const (
    FACTOR_P  = 0.25
    MAX_LEVEL = 32
)

type SkiplistNode struct {
    Val int
    Forward []*SkiplistNode
}

type Skiplist struct {
    head *SkiplistNode
    level int
}

初始化

初始化将头结点的Forward长度设置为MAX_LEVEL，当前层级设计为1（你要设置为0也可以），Forward[0]设置为空。

func NewSkiplist() *Skiplist {
    return &Skiplist{
        head: &SkiplistNode{0, make([]*SkiplistNode, MAX_LEVEL)},
        level: 1,
    }
}

随机层级

根据随机因子p=0.25，节点出现第i层的概率为：(1-p) x p^i-1，实现为：

func (this *Skiplist) randomLevel() int {
    rnd := rand.New(rand.NewSource(time.Now().UnixNano()))
    level := 1
    for level < MAX_LEVEL && rnd.Float64() < FACTOR_P {
        level++
    }
    return level
}

查找

查询比较简单，从头节点开始，至顶层开始，如果当前层的Forward指针指向节点的值小于目标值，向Forward指针方向前进，一直到最底层。节点最底层的下一个节点存在，且其值正好等于目标值，则找到，否则目标值不存在。

func (this *Skiplist) Search(target int) bool {
    curr := this.head
    // 从上往下遍历
    for i := this.level - 1; i >= 0; i-- {
        // 找到距离target最近的节点
        for curr.Forward[i] != nil && curr.Forward[i].Val < target {
            curr = curr.Forward[i]
        }
    }

    curr = curr.Forward[0]
    return curr != nil && curr.Val == target
}

插入

插入时，需要先按照查找的方法，找到要插入的位置。在这个过程中需要用一个update向量记录插入时需要更新的结点。udpate[i]表示指向第i层最右侧节点的指针，指针指向被插入的或更高的位置。如下图：

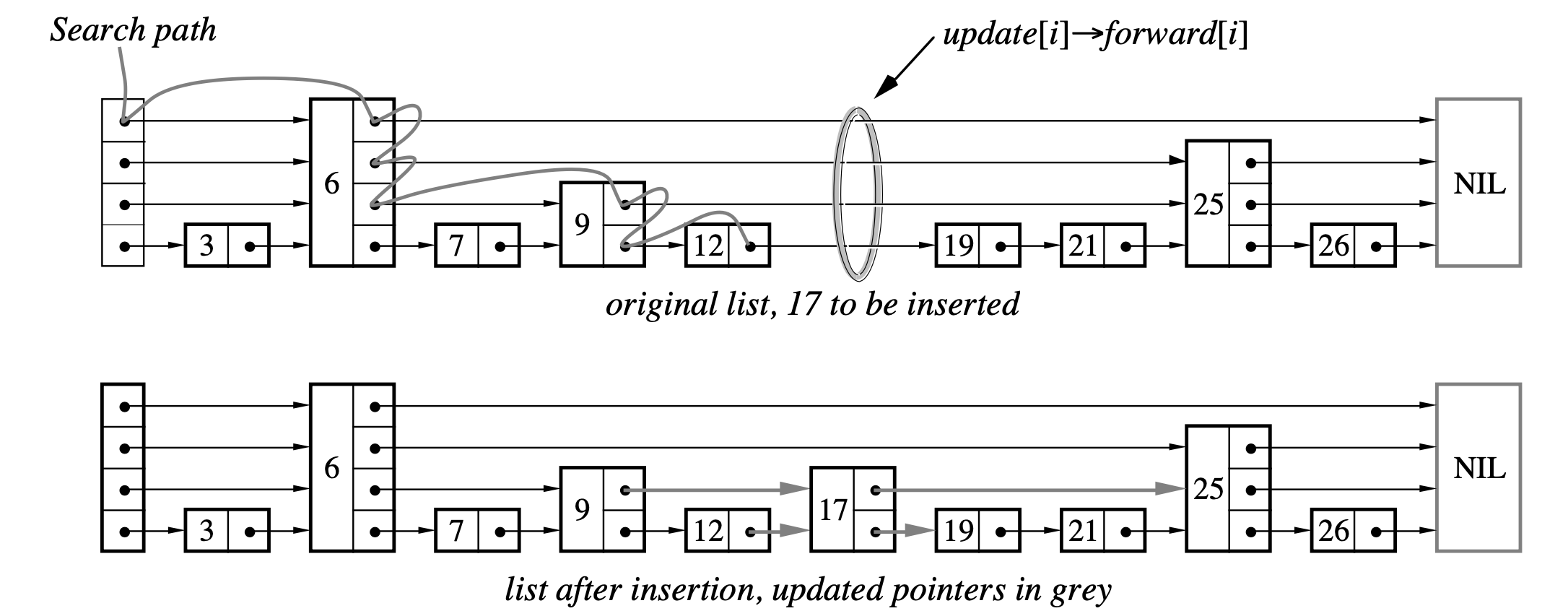
生成新节点时，会生成一个随机层级，如果这个新生成的层级超过了当前跳跃表的层级，还需要更新当前跳跃表的层级，并将update向量大于跳跃表层级的向前指针设置为head。

func (this *Skiplist) Insert(num int)  {
    update := make([]*SkiplistNode, MAX_LEVEL)
    curr := this.head
    for i := this.level - 1; i >= 0; i-- {
        for curr.Forward[i] != nil && curr.Forward[i].Val < num {
            curr = curr.Forward[i]
        }
        update[i] = curr
    }

    lvl := this.randomLevel()

    // 新生成的层级大于跳跃表的层级
    if lvl > this.level {
        for i := this.level; i < lvl; i++ {
            update[i] = this.head
        }
        this.level = lvl
    }

    // 插入新节点
    newNode := &SkiplistNode{num, make([]*SkiplistNode, lvl)}
    for i := 0; i < lvl; i++ {
        newNode.Forward[i] = update[i].Forward[i]
        update[i].Forward[i] = newNode
    }
}

删除

删除和插入的逆操作，主要区别有以下两点：

update向量第i层向前指针如果指向目标节点，则只需要将update[i].Forward[i]指向target.Forward[i]即可。
删除目标节点后，由于目标节点可能具有最大层级，删除后，需要更新跳跃表维护的层级。

func (this *Skiplist) Delete(num int) bool {
    update := make([]*SkiplistNode, MAX_LEVEL)
    curr := this.head
    for i := this.level - 1; i >= 0; i-- {
        for curr.Forward[i] != nil && curr.Forward[i].Val < num {
            curr = curr.Forward[i]
        }
        update[i] = curr
    }

    target := curr.Forward[0]
    // 未找到目标节点
    if target == nil || target.Val != num {
        return false
    }

    // 删除target结点
    for i := 0; i < this.level && update[i].Forward[i] == target; i++ {
        update[i].Forward[i] = target.Forward[i]
    }

    // 更新层级
    for this.level > 1 && this.head.Forward[this.level - 1] == nil {
        this.level--
    }
    return true
}

完整代码参考: github。

参考资料

[1] Skip Lists: A Probabilistic Alternative to Balanced Trees
[2] 维基百科