LeeYzero的博客

自强不息，厚德载物

0%

Go json.Unmarshal 精度丢失问题分析（2/2）

Posted on Edited on In

缘起

最近出现一例json.Unmarshal导致的精度丢失引发的线上问题，虽然这个问题在被及时发现，未对业务造成损失，但细挖这个问题的原因仍然比较有意思。这篇文章会从技术层面深入分析json.Unmarshal精度丢失的原因以及处理建议，以避免后续开发过程中再次踩坑。

在 Part1 中，我们着重说明了json.Unmarshal处理大整数可能出现精度丢失的问题，但遗留了一个问题，即大整数置换成浮点数时，为什么会造成精度丢失，在这篇文章中我会详细解释原因。

Go语言对浮点数的处理遵循IEEE-745标准，该标准规定了浮点数在计算机中的二进制表示以及舍入方式，下面先补充一些基础知识，然后再结合 Part1 中的case，分析精度丢失的原因。

十进制与二进制

十进制用0-9表示，逢十进一，同时二进制用0和1表示，逢二进一。而每个位可以使用位的值乘以位的权重表示，直接看例子：

十进制12.34可以表示为：
12.34 = 1×101 + 2×100 + 3×10−1 + 4×10−2 = 12.34

同理二进制101.11也可以表示为：

101.11 = 1×22 + 0×21 + 1×20 + 1×2−1 + 1×2−2 = 4 + 0 + 1 + 1/2 + 1/4 = 5.75

十进制小数点向左移动1位相当于将该数除以10，向右移动1位相当于将该数乘以10。
例如：123/10 = 12.3，12.3×10 = 123。

同理，二进制小数点向左移动1位相当于将该数除以2，向右移动1位相当于将该数乘以2。

例如：11/2 = 1.1，1.1x2 = 11

科学记数法

科学记数法，是一种数字的表示法，用于表示极大或极小的数。例如：

0.00000000000000000000000167262158 = 1.67262158×10−24
1898130000000000000000000000 = 1.89813×1027

等号右边就是科学记数法的表示格式，即：a×10n

其中：

  • |a|>=1 且 |a|<10
  • n为整数

二进制的科学记数法同理，即：ax2n
其中：

  • |a|>=1 且 |a|<2
  • n为整数

举个例子，看看如何将二进制数表示为科学记数法的格式。

5.7510 = 101.112 = 1.01112×22（小数点向右移动1位相当于将该数乘以2）

IEEE-745

在计算机中，浮点是一种对于实数的近似值数值表示法，由一个有效数字（即尾数）加上幂数来表示，通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值，称为浮点数。可以简单理解为：浮点数是十进制科学记数法在计算机中的二进制表示，即二进制的科学记数法。

IEEE-745标准化了计算机中浮点数的表示方法，内容比较多，这里主要讲解浮点数的表示和浮点数的舍入。

浮点数的表示

IEEE-745标准用 V = (-1)s x M x 2E 的形式来表示，其中：

  • 符号（sign）：s决定这个数是正数（s=0）还是负数（s=1）
  • 阶码（exponent）：E的作用是对浮点数加权，这个权重是2的E次幂（可能是负数）
  • 尾数（signifcand）：M是一个二进制小数，用于存储“有效数字”的小数部分。

将浮点数的位表示划分为三个域，分别对这些域进行二进制编码：

  • 1位符号域，直接编码符号s，0表示正数，1表示负数。
  • k位阶码域，exp = ek-1 … e1e0 编码阶码E，规定为实际指数值加上一个偏移值，偏移值为2k-1 - 1，k为存储指数的比特位长度。
  • m位小数域, frac = fm-1 … f1f0 编码尾数M，使用原码表示。

IEEE745 规定了四种表示浮点数值的方式，但常用的是单精度（32位）和双精度（64位）。它们的二进制bit位，s、exp和frac字段位分别为：

  • 单精度浮点格式：n=32位、s=1位、k=8位、m=23位。
  • 双精度浮点格式，n=64位，s=1位，k=11位，m=52位。
image

举个例子，我们将整数78转换成64位浮点数表示应该是多少呢？

  1. 将78表示成二进制数：1001110，浮点数表示为1.001110 x 26
  2. 分别对三个字段进行二进制编码
  • 符号位（1位）：78为正数，符号位编码为0
  • 阶码位（11位）：指数为6，阶码值为：实际指数 + 偏移量 = 6 + 211-1 - 1 = 6 + 1023 = 1029 = 10000000101
  • 小数位（52位）：1.001110中整数部分始终为1，不显示表示，小数部分001110直接使用52位原码表示为：0000000000000000000000000000000000000000000000001110

所以78的浮点数二进制表示为：

1
0 - 10000000101 - 0000000000000000000000000000000000000000000000001110

你可以有些疑问，为什么阶码需要加一个偏移量？偏移量为什么是2k-1 - 1而不是2k-1。这些问题会引入更多问题，仅对分析这个case来讲没有太大帮助，在此只做简单解释，不展开。

为什么阶码需要加一个偏移量？
阶码的定义是有符号的，加上一个偏移可以将负值平移至正整数空间，这样阶码的计算就不用关心符号了，这有利于计算机做比较运算。

偏移量为什么是2k-1 - 1而不是2k-1？
上面例子中浮点数的表示只是浮点数的规格化表示，标准中对于k位的阶码为全0或全1时，用于表示非规格化和特殊值。规则如下：

形式 指数 小数部分
零 0 0
规格化形式 [1, 2k - 2] [1, 2)
非规格化形式 0 (0, 1)
无穷 2k - 1（全1） 0
NaN 2k - 1（全1） 非0

浮点数的舍入

浮点数的表示限制了浮点数的范围和精度，浮点数运算只能近似地表示实数运算。比如0.2可以用实数精确表示，但不能用二进制精确表示，它的二进制为0.001100110011……（0011循环）。

因此对于一个数值，如果不能精确表示时，需要找到最接近的值进行表示，这就是舍入(rounding）。IEEE 745规定了四种舍入方式。默认方式是偶数舍入（round-to-even)，也称为向最接近的值舍入（round-to-nearest）。

比如将金额舍入到最接近的整数元时，将1.40元舍入为1元，1.60舍入成2元，而1.50距离1和2都一样，此是向偶数合入，所以1.50和2.50都舍入为2元。

其它舍入方式如下：

方式 1.40 1.60 1.50 2.50 -1.50
向偶数舍入 1 2 2 2 -2
向零舍入 1 1 1 2 -1
向下舍入 1 1 1 2 -2
向上舍入 2 2 2 3 -1

分析

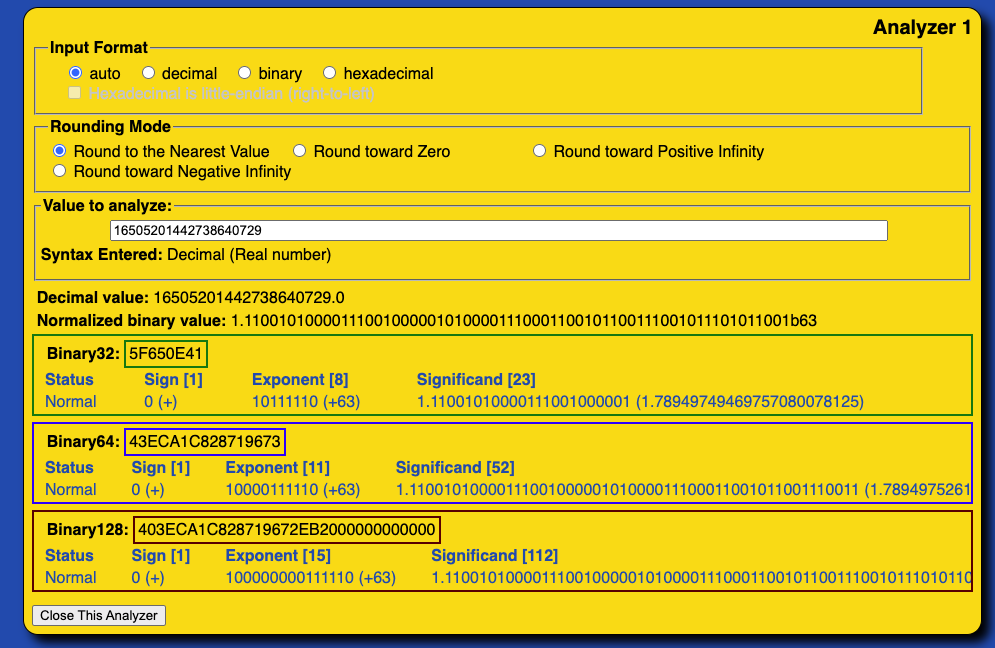
有了上面的背景知识，我们再回到这个case。分析为什么大整数16505201442738640729不能用float64精确表示。

这篇文章中提到“float64可存储的最大整数是小于int64”的结论其实是错误的，float64能表示的范围非常大（可以看下math.MaxFloat64有多大）。这里的主要问题在于float64并不能精确的表示所有int64的值，下面我们来看看为什么会是这样。

大整数16505201442738640729的二进制表示为：

1
fmt.Printf("%.064b\n", uint64(16505201442738640729))

上述代码输出：

1
1110010100001110010000010100001110001100101100111001011101011001

使用浮点数表示为：
1.110010100001110010000010100001110001100101100111001011101011001 x 263

下面来看它在内存中的二进制如何表示：

  • 符号位（1位）：正数，0
  • 阶码位（11位）：指数为63，阶码值为：实际指数 + 偏移量 = 63 + 211-1 - 1 = 63 + 1023 = 1086 = 10000111110
  • 小数位（52）：小数中一共有63位，但小数位只有有52位，需要进行截断，如下（空格后是需要截断的小数位）
1
1100101000011100100000101000011100011001011001110010 11101011001

发生截断会导致精确丢失，需要进行舍入，上述小数位向下舍入为：

1
1100101000011100100000101000011100011001011001110010 (对应的十进制值为：16505201442738638848）

向上舍入为：

1
1100101000011100100000101000011100011001011001110011（对应的十进制值为：16505201442738640896）

注：Go标准库math包中提供了一个函数Float64frombits，可以计算出向下舍入和向上舍入后的float64值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func MakeFloat64FromBits(sign1 uint32, exp11 uint32, frac52 uint64) float64 {
    sign := (uint64(sign1) & 0x1) << 63
    exp := (uint64(exp11) & 0x7ff) << 52
    frac := frac52 & 0xfffffffffffff
    bit := sign | exp | frac
    return math.Float64frombits(bit)
}

func main() {
    f1 := MakeFloat64FromBits(0, 1086, 0xca1c828719672)
    fmt.Printf("向下舍入: %f\n", f1)

    f2 := MakeFloat64FromBits(0, 1086, 0xca1c828719673)
    fmt.Printf("向上舍入: %f\n", f2)
}

输出为：

1
2
向下舍入: 16505201442738638848.000000
向上舍入: 16505201442738640896.000000

根据向偶数舍入规则，大整数16505201442738640729离16505201442738640896更近，所以小数位的二进制最终表示为：

1
1100101000011100100000101000011100011001011001110011。

最终我们得到16505201442738640729使用浮点数表示后，在内存中的二进制布局为：

1
0 - 10000111110 - 1100101000011100100000101000011100011001011001110011

至此，我们已经清楚，为什么16505201442738640729转换成浮点数会丢失精度了。但在Go语言中，大整数16505201442738640729的浮点表示，在内存中的布局是不是这样呢？我们可以使用math包中提供了一个函数Float64bits，可以将float64的浮点数转换成uint64的二进制数。

1
2
3
4
5
6
7
8
9
10
11
func PrintFloat64Bit(f float64) {
    bits := math.Float64bits(f)
    binary := fmt.Sprintf("%.64b", bits)
    // 符号位、指数位、小数位
    fmt.Printf("%s | %s | %s\n", binary[0:1], binary[1:12], binary[12:64])
}

func main() {
    f := float64(uint64(16505201442738640729))
    PrintFloat64Bit(f)
}

输出结果：

1
0 | 10000111110 | 1100101000011100100000101000011100011001011001110011

可以看出，大整数16505201442738640729的浮点表示在内存中的布局跟上面计算的结果是一致的。如果再进一步分析，可以看到，Go中strconv.ParseFloat的实现采用了The Eisel-Lemire ParseNumberF64 Algorithm，该算法将字面量转成双精度浮点数，其主要目标是为了速度，但算法实现比较复杂，感兴趣的可以深入学习。

分析工具

上面例子中我们通过人工或代码实现进行分析，主要是为了加深理解，其实已经有现成的工具IEEE-754 Analysis帮助我们分析。

image

参考资料