Leslie Lamport 在1978年发表了一篇论文Time, Clocks, and the Ordering of Events in a Distributed System,对分布式系统领域产生的深远影响,这篇论文也成为分布系统领域引用最高的文献之一。
论文中定义了分布式系统中事件的”happen before”关系,并引入了逻辑时钟解决分布式系统中事件同步的问题。但由于系统之外的信息传递并不受系统内部逻辑时钟的约束,所以会出现因果不一致的问题。于是论文中又提出物理时钟,只要能保证各进程中物理时钟同步在一个合理误差范围内,就能保证系统的全局排序。
读完后,除了对分布式系统中事件同步有了新的认识外,也对系统设计有了一些新的思考。这篇文章主要对论文做一些解读并谈谈自己的解理。
相对论的启示
据Leslie Lamport本人回忆,当他看到Paul Johnson和Bob Thomas的论文The Maintenance of Duplicate Databases中使用时间戳来提供分布式系统中的全局一致性时,他立即看出了算法中存在的问题。他之所以能够一下看出其本质,原因在于他对相对论有深刻的认识:
Special relativity teaches us that there is no invariant total ordering of events in space-time; different observers can disagree about which of two events happened first. There is only a partial order in which an event e1 precedes an event e2 iff e1 can causally affect e2.
狭义相对论告诉我们,时空中事件不存在绝对的全局顺序;不同的观察者可能对两件事件中哪件先发生持有不同的看法。事件在时空中只存在部分有序,只有当 e1 对 e2 产生因果影响时,事件 e1 才先于事件 e2。
在相对论中,这叫做同时相对性,这里我们不用深究其原理。有一个著名的火车思想实验,能够帮忙我们更直观理解。
在火车与月台上,分别有两个观察者。观察者A站在火车的正中央,观察者B站在月台上。当两名观察者相遇时,一道闪光从火车的中央发出。
对火车上的观察者A而言,由于火车头和火车尾和光源的距离是固定的,所以光会同时抵达火车头和火车尾。
对月台上的观察者B而言,火车尾会朝向闪光的发射点靠近,火车头则会远离闪光发射点。由于光速是固定的,光到火车尾的距离比到火车头的距离要短。因此B认为光会先到达火车尾,后到达火车头。
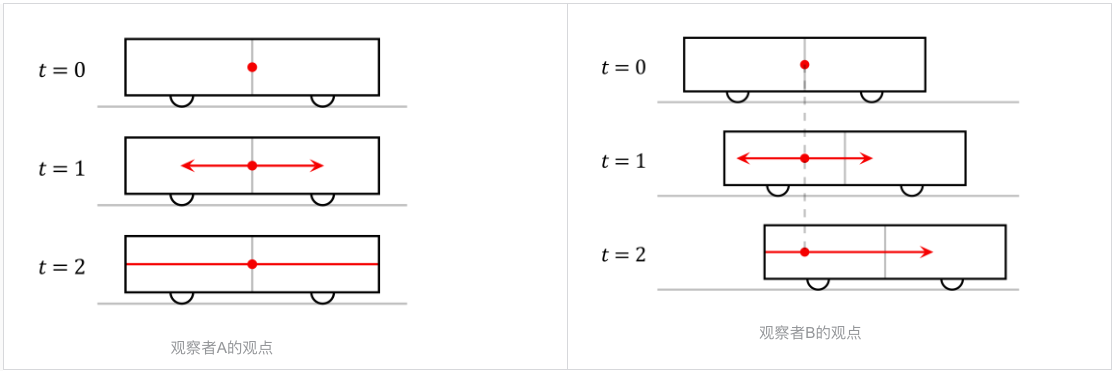
这个实验告诉我们,对于不同参考系的观察者而言,事件的顺序并没有一致的结论。但这并不意味着因果上的逻辑矛盾,如果事件A的发生是因,导致事件B发生,则事件B是果,在这种情况下,因果事件的顺序是确定的,这就是上面提到的部分有序。
如何理解因果一致性呢?可以想象一下,如果事件A发生了,A对B要产生影响,那么A事件的信息(光速)要传递到B,必定要经过一定的距离(空间),因为光速是固定的,所以必定要经过一定的时间才能到达B,所以A事件发生在B事件之前,A和B的关系即论文里提到的 happen before。
偏序和全序
上面说的全局有序和部分有序,在序理论中有两种形式化的描述:偏序(Partial Orderding) 和 全序(Total Ordering)。这里需要简单补充一下背景知识,有点乏味,但比较容易理解。
偏序
偏序在数学上是一种特殊的二元关系,给定集合S,假设 ≤ 是S上的二元关系,如果 ≤ 满足:
- 自反性:对S中的任意元素a,有 a ≤ a;
- 反对称性:对S中的任意元素a、b,如果 a ≤ b 且 b ≤ a,则a = b;
- 传递性:对S中的任意元素a、b、c,如果 a ≤ b 且 b ≤ c,则 a ≤ c;
这是数学上对偏序的定义,可以简单理解为:偏序关系是一种序关系,但只有部分元素有序,并不是全部元素都可以比较。 比如,文件系统中的文件和文件夹的包含关系就是一个偏序关系:
- 自反性:一个文件夹包含自己
- 反对称性:如果文件夹A包含文件夹B,那么B就不包含A。
- 传递性:如果文件夹A包含文件夹B,B包含文件夹C,那么A也包含C。
而两个同级目录下的文件夹,它们没有包含关系,所以并不能比较。
全序
全序比偏序更加严格一些,它只在偏序的基础上多了一个完全性条件:
- 完全性:对于S中的任意元素a和b,必须有 a ≤ b 或 b ≤ a;
可见,全序是在偏序的基础上,要求全部的元素都可以比较。比如,对于整数集合,任意两个数都是可以比较的;又比如单词的字典序也是一个全序关系,任意两个单词都可以根据字母顺序进行比较。
总的来说,偏序关系中集合中的元素部分可比较;全序关系中集合中的元素都可以比较。形象地说,偏序关系就像是一棵树,不同分支上的元素可能无法直接比较;而全序关系就像是一条直线,所有元素都按顺序排开。
Happen Before
说了这么多,终于进入主题了。上文提到,作者从狭义相对论中得到启示:时空中没有绝对的全序关系,只存在偏序关系。这跟分布式系统有什么关系呢?
A distributed system consists of a collection of distinct processes which are spatially separated, and which communicate with one another by exchanging messages.
分布式系统是由一系列空间上分离的进程组成,这些进程通过交换消息进行通信(产生了因果关系)。
跟现实世界类似,在分布式系统中,每个进程都是相对独立的,它们在自己的视角下接收信息和发送信息。分布在两个不同进程中的事件,我们很难说哪个事件先发生(见上文的同时相对)。只有当一个进程收到另一个进程发送的消息时,他们之前就出现了happen before关系。可以看出,这里的happen before关系,跟偏序关系是一致的,于是作者对happen before也做了形式化的定义:
使用 “→” 表示happen before关系。事件a在事件b之前发生表示为 a → b,那么有:
- 如果 a 和 b 是同一个进程内的事件,且a在b之前发生,则 a → b;
- 如果事件 b 接收到事件 a 发送的消息,则 a → b;
- 如果 a → b 并且 b → c,那么 a → c;
如果事件a和事件b是并发的,记为 a || b。
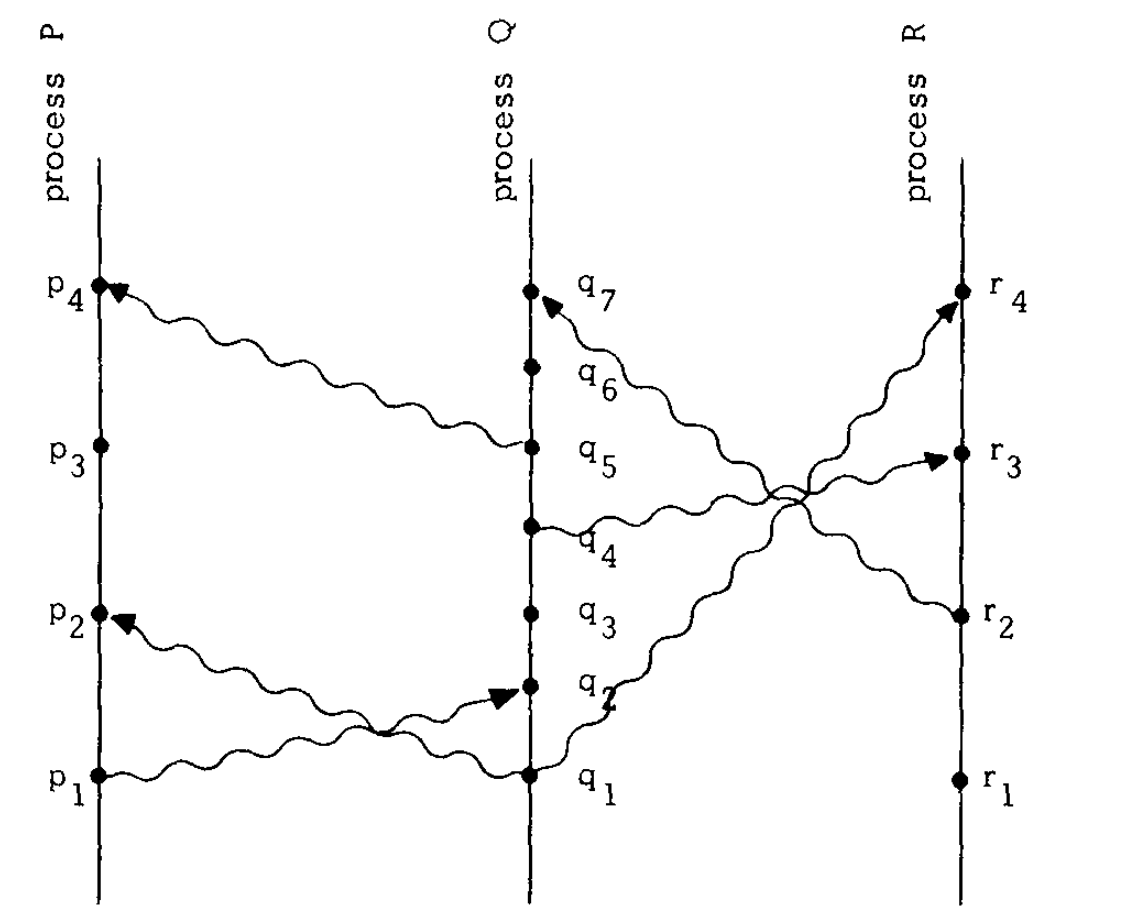
如上图中,横坐标表示空间,纵坐标表示时间,箭头表示消息传递,我们说:
- p1 → r4:p1和r4有happen before关系,因为p1 → q2 → q4 → r3 → r4
- p3 || q3:p3和q3是并发的,因为他们之间没有消息传递,无法定义他们的先后顺序。
当前说的时间是物理时间,但在分布式系统中,由于机器之间的时钟频率差异,以及时钟同步受网络延迟的影响,会造成各机器的时间存在差异。所以在分布式系统中,当进程收到消息时,不能以本地时间作为物理时间来判断事件的先后顺序。
但我们真的需要物理时间吗?
We begin with an abstract point of view in which a clock is just a way of assigning a number to an event, where the number is thought of as the time at which the event occurred.
从抽象的观点来看,时钟只是为事件分配数字的一种方式,其中数字被认为是事件发生的时间。
于是作者引入了逻辑时钟(Logical Clock),一种独立于物理时钟时间,为事件分配数字的一种方式。
逻辑时钟
逻辑时钟特意避开了物理时间。只要事件的逻辑时钟能够满足happen before关系,我们就可以对事件进行排序。那什么是逻辑时钟呢?
逻辑时钟相当于一个函数,对于每一个发生的事件,它都能分配一个对应的数字(相当于给事件打上一个时间戳)。逻辑时钟C(a):表示事件a发生时对应的时钟值。当然要满足Happen before关系,生成的时钟值也是有条件的,于是作者定义了一个时钟条件(Clock Condition):
对于任意事件a和b:如果 a → b,那么必须满足C(a) < C(b)
从happen before关系可以很容易的看出,只要时钟条件遵循以下两个条件,就能满足happen before关系。其中Ci(a)表示进程Pi中事件a的逻辑时钟。
- 如果事件a和b在同一进程Pi中,且a发生在b之前,则:Ci(a) < Ci(b)
- 如果进程Pj中的事件b收到进程Pi中的事件a发送的消息,则:Ci(a) < Cj(b)
遵循这两个条件比较简单,作者给出一种逻辑时钟算法:
1 | 1. 每个进程Pi内维护本地一个计数器Ci,初始为0; |
下图是逻辑时钟算法的示意图,最后进程Pi和Pj的逻辑时钟为:Ci = 6,Cj = 5
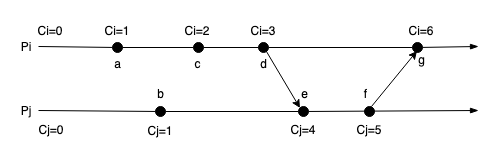
在这个例子中:
- 进程Pi经过了事件a,b,c后,逻辑时钟变为Ci=3,然后在事件d发送消息给进程Pj,消息中携带Pi的逻辑时钟Ci=3。
- Pj经过一个事件b后,逻辑时钟Cj=1,当在e收到消息时,根据逻辑时钟算法,Cj = max(Ci,Cj) + 1 = 4
- Pj在事件f中,Cj = Cj + 1 = 5,并将逻辑时钟Cj=5随消息发送给Pi
- Pi在事件g中,收到Pj的消息,根据逻辑时钟算法,Ci = max(Ci,Cj) + 1 = 6
根据上述时钟条件,如果a → b,那么可以得到C(a) < C(b)。但如果C(a) < C(b),能不能得出 a → b呢?可惜,答案是否定的。
比如上图中的Cj(b) < Ci(c)的,但事件b和事件c是一个并发关系,即b || c。主要原因在于事件a和事件b并不相关,它们没有因果关系(没有互通消息,或者说没有被观察到),它们之间没有可比较性,这其实是偏序的一种体现。
至此,我们发现一个矛盾的问题:时钟条件是单向的,也就是说知道事件a happen before b,必定有C(a) < C(b),但反过来却不成立。但在一个分布式系统中,我们通过需要根据时间来判断事件的先后顺序。我们能不能从C(a) < C(b)推导出事件a happen before 事件b呢?
于是作者引入了全序(Total Ordering),全序关系用符号=>表示:
a => b 表示系统中任意事件a happen before 事件b。
对进程Pi中的事件a和进程 Pj中的事件b,如果要满足全序关系a => b,只需要满足以下两个条件即可:
- 条件1:Ci(a) < Ci(b) 或者
- 条件2:Ci(a) = Ci(b) and Pi < Pj
什么意思呢?作者给了比较详细的形式化定义。简单来说就是对于并发的事件,既然不知道谁先发生,那就人为给他们指定一下顺序。指定顺序满足上述两个条件即可。
仍然以上图为例,根据happen before关系,有:
Ci(a) < Ci(c) < Ci(d) < Cj(e) < Cj(f) < Ci(g)
而事件b和事件a、c、d都是并发的,对于并发的事件,如果它们的逻辑时钟可以比较(条件1),则以逻辑时钟大小排序,如果逻辑时钟相同,按进程号排序(条件2),由于Pi < Pj,于是我们得到事件的全序关系:
Ci(a) < Ci(b) < Ci(c) < Ci(d) < Cj(e) < Cj(f) < Ci(g)
逻辑时钟的应用
全序关系有什么用呢?作者在采访中说:
It didn’t take me long to realize that an algorithm for totally ordering events could be used to implement any distributed system. A distributed system can be described as a particular sequential state machine that is implemented with a network of processors. The ability to totally order the input requests leads immediately to an algorithm to implement an arbitrary state machine by a network of processors, and hence to implement any distributed system. So, I wrote this paper, which is about how to implement an arbitrary distributed state machine. As an illustration, I used the simplest example of a distributed system I could think of–a distributed mutual exclusion algorithm.
我很快意识到,全序事件算法可用于实现任何分布式系统。分布式系统可以描述为通过网络实现的特定顺序状态机。全序输入请求的能力可以立即推导出通过处理器网络实现任意状态机的算法,从而实现任何分布式系统。因此我写了这篇论文,内容是关于如何实现任意分布式状态机。为了说明这一点,我使用了我能想到的最简单的分布式系统示例——分布式互斥算法。
那么我们来看一下,全序关系如果实现分布式锁。首先从正确性上来描述,分布式锁要满足以下三个条件:
- 1)获得锁的进程必须释放锁后,其它进程才能获得锁,这是互斥性,保证资源最多只能被一个进程访问;
- 2)不同进程获得锁的顺序必须和请求的顺序一致;
- 3)如果每个进程最终都会释放锁,那么所有进程发出的锁请求最终都能满足;
在常见的分布式锁实现中,都是通过中心化服务器来控制锁的获取和释放(比如用MySQL或Redis),但中心化服务器容易受网络延迟的影响导致违反条件2。如下:
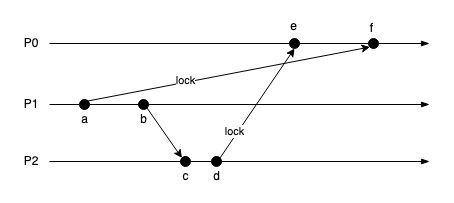
P0是中心服务器,P1发送一个锁请求给P0,然后P1发送消息给P2,P2收到消息后,给P0也发送锁请求,但由于网络延迟,P2的请求比P1的请求先到P0,导致P2先获得锁。这其实是违背因果一致性的。
于是,作者给出一个分布式互斥算法,这个算法没有中心服务器。具体方案是,每个进程在本地维护一个逻辑时钟,逻辑时钟的更新算法上文已经介绍过了。同时维护一个队列,队列中每个元素是一个二元组<Tm, Pi>,其中Tm是消息发送时的本地逻辑时钟,Pi是进程i的进程 号。方案假设消息可以延迟,但最终一定能到达。算法如下:
1 | 1. 如果进程Pi需要获取锁,发送<Tm, Pi>消息给其它所有进程; |
来看个例子:
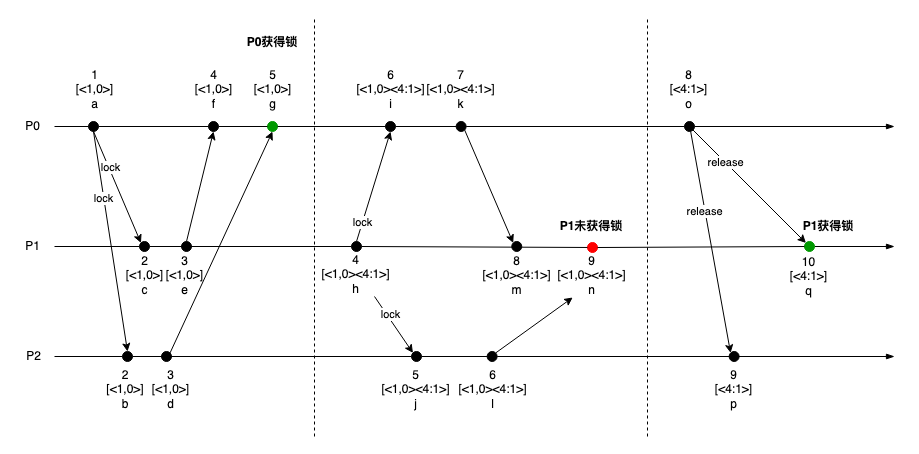
每个事件中,每一行表示本地逻辑时钟Tm,第二行表示本地队列,每项为<Tm, Pi>,第三行表示事件节点。
1 | 1. P0进程在事件a发出锁请求给P1和P2,消息内容为<1,0>; |
再来看下该算法如何解决的因果顺序的问题,如下图所示:
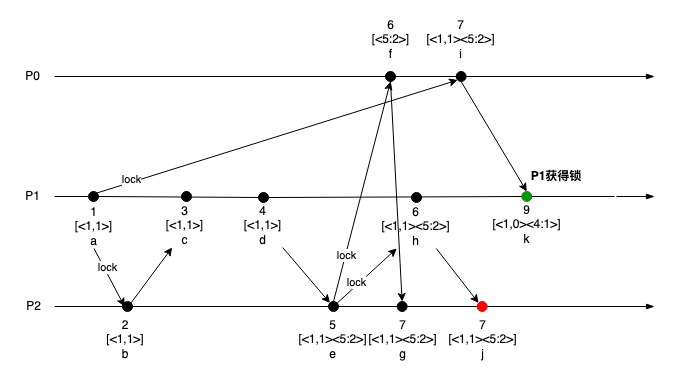
在这个例子中,事件节点a和事件节点e是存在因果关系的。P1在节点a发起锁请求,由于网络延迟P0在i结点才收到P1的锁请求。P2在e节点发起锁请求,虽然在j节点收到了所有进程的ACK消息,但并不满足算法3.1,所以P2在j结点并不能获得锁。
在这个算法中,没有中心服务器,每个进程独立运行上述算法,是一个真正的分布式锁。但这个算法比较理想,在工程实现上却有很多问题,比如如何指定进程号大小?其中某个进程挂了怎么办?消息丢了怎么办?这些问题都是现实中存在的客观问题,作者在论文中并未给出解决办法。
逻辑时钟的异常行为
逻辑时钟除了上节提到的工程问题外,但存在着异常行为。来看个例子:
Alice和Bob住在两个不同城市。Alice在网络上观看世界杯,当Alice看到甲队进球后比分为1:0,给Bob打电话告诉他这个消息。Bob打开手机查看比赛,发现比分还是0:0,这便是作者在论文中说的异常行为。
在这个例子中,我们假设网络电视后端是一个分布式系统,使用逻辑时钟进行同步。在系统内部使用逻辑时钟是满足事件的偏序关系,Alice看到最新比分后,给Alice跟Bob打电话,Alice跟Bob在系统外(现实世界)也建立了一种偏序关系。之所有出现这种异常行为是因为基于逻辑时钟建立偏序关系的内部系统和跟基于物理时间建立偏序关系的现实世界存在联系了。
一种办法是让内部系统跟外部系统通信时让外部系统也携带逻辑时钟,相当于将所有外部系统都纳入到系统的逻辑时钟体系内。显示这种办法是不现实的,于是作者提出物理时钟(Physical Clock)。
物理时钟
作者对物理时钟也做了严格的定义和证明,证明过程比较复杂,这里只介绍核心思想。
物理时钟的提出主要用于解决上节提到的异常行为。上节提到系统内部和系统外是基于不同的时间(时钟)建立偏序关系,当系统内部和系统外部有联系时,两个系统中的偏序关系是不兼容。如果我们有一种物理时钟同步算法,能够让时钟同步的速度快于外部消息传递的速度,那么问题就解决了。
那么要快到什么程度呢?答案是光速,因为信息传播的速度上限就是光速。
物理时钟同步算法通过在时钟之间不断交换信息并按照一定规则调整时钟读数,将时钟误差控制在一定范围内,并且时钟不能出现倒退现象。这就是作者定义的强时钟条件(Strong Clock Condition)。
再回到上面的例子,如果系统使用物理时钟,且物理时钟同步在非常小的误差范围内。即使外部信息传递再快(信息传递最快的物理极限是光速),也不会出现异常行为了。
总结
论文中有很多形式化的定义(作者很擅长这个),但我觉得这些都不重要,最重要的是意识到在一个分布式系统中,事件的顺序只存在偏序关系。关于这篇论文,还有一个很有意思的事情,作者在一次采访中提到,许多人认为这篇论文是在讲分布式系统的因果关系,或者是分布式互斥问题,但很少有人知道这篇论文里提到了状态机。这让他不得不回过头来重读它,以说服自己确实写过相关内容(作者确实有提到)。
这篇论文对分布式领域影响深远,对于逻辑时钟,应用很广泛,比如Raft算法中领导人选举其实本质上就是一个逻辑时钟。但逻辑时钟中事件的happen before和时钟大小是一个充分不必要条件,后续又有人提出了向量时钟解决了这个问题,这篇文章中讲得比较清楚;对于状态机的思想,也被广泛应用于主备复制的复制状态机之中;关于物理时钟,Google为spanner系统设计的TrueTime其实就是应用了这个原理。
除了论文中提出的很多原创性思想外,关于作者解决问题的思路也是非常值得我们学习的。在关于分布式系统中的事件同步问题上,作者洞析了事件顺序的本质——偏序关系,并对时间作了抽象,提出逻辑时钟,使其在系统内是逻辑自洽的。当系统的约束不能满足需求时,又跳出当前系统,从更高一个维度看态问题并解决问题,提出了物理时钟。这里除了作者拥有深厚的跨学科功底外,也隐含了解决问题的普适方法:
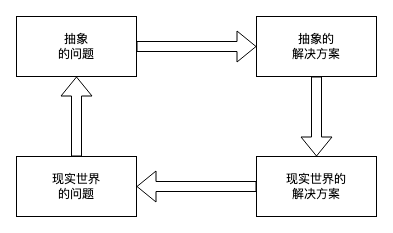
对于现实世界的复杂问题,我们就需要将问题的本质进行抽象,然后映射到一个模型上,在模型内解决问题,再将解决方案转换为现实世界的方案,当新的问题出现,系统不能自洽处理,说明底层模型已经不能解决当前问题,于是需要跳出当前模型,重新对问题建模,重复上述过程。